
For a full list of BASHing data blog posts see the index page. ![]()
Making a transect into a point and circle
In a BASHing data blog post last month I featured the WKT format, which can be used to describe a straight-line transect from latitude/longitude point 1 to latitude/longitude point 2:
LINESTRING (longitude1 latitude1, longitude2 latitude2)
Another way to describe a straight-line transect is with its midway point plus the radius of a circle which includes the whole of the transect. In the Darwin Core scheme for recording biological data, that midway point is at decimalLatitude and decimalLongitude, and the circle's radius, or half the length of the transect, is the coordinateUncertaintyInMeters.
Given the LINESTRING WKT for a transect, you can calculate the midway point and half the transect length in a single AWK command, as explained below.
As a demonstration file ("wkts") I'll use 10 marine sampling transects from a GBIF dataset:
LINESTRING (-42.98106 -60.74496, -42.98813 -60.74046)
LINESTRING (-44.99019 -62.15421, -44.98773 -62.14981)
LINESTRING (-44.99531 -62.28379, -45.00127 -62.28109)
LINESTRING (-45.64496 -62.66805, -45.64785 -62.66019)
LINESTRING (-46.52195 -60.36142, -46.53308 -60.35873)
LINESTRING (-46.53158 -60.36383, -46.53119 -60.35797)
LINESTRING (-46.68411 -60.35385, -46.68745 -60.35828)
LINESTRING (-46.68423 -60.35437, -46.68761 -60.35889)
LINESTRING (-46.68984 -60.22065, -46.69883 -60.21816)
LINESTRING (-46.76719 -60.32237, -46.77263 -60.32624)
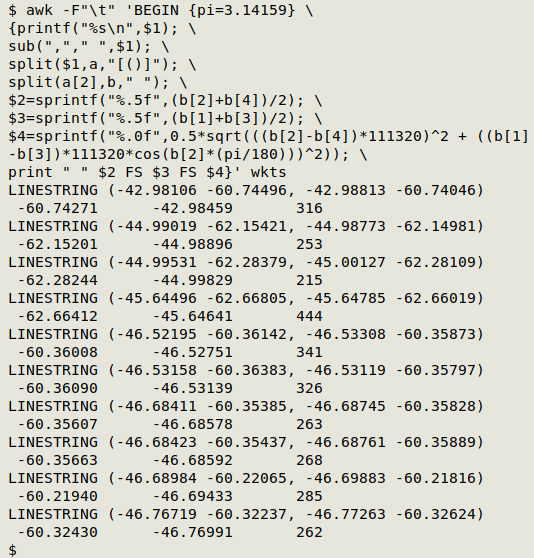
The command I'll use prints decimalLatitude, decimalLongitude and coordinateUncertaintyInMeters as tab-separated items. For display purposes I'll put the results on a new line and slightly indent them. Here's that command and its output with "wkts":
awk -F"\t" 'BEGIN {pi=3.14159} \
{printf("%s\n",$1); \
sub(","," ",$1); \
split($1,a,"[()]"); \
split(a[2],b," "); \
$2=sprintf("%.5f",(b[2]+b[4])/2); \
$3=sprintf("%.5f",(b[1]+b[3])/2); \
$4=sprintf("%.0f",0.5*sqrt(((b[2]-b[4])*111320)^2 + ((b[1]-b[3])*111320*cos(b[2]*(pi/180)))^2)); \
print " " $2 FS $3 FS $4}' wkts
-F"\t" AWK is told that the input field separator is a tab. Since there are no tabs in "wkts", the whole WKT becomes field 1.
BEGIN {pi=3.14159} AWK doesn't have pi as an internal constant, so it's added here as a variable in a BEGIN statement.
{printf("%s\n",$1);AWK's first action is to printf the WKT, followed by a newline. In a tab-separated data table, it would instead be followed by a tab.
sub(","," ",$1); Here AWK replaces the comma in the LINESTRING with a plain space, modifying the field.
split($1,a,"[()]");The modified field 1 is split using either "(" or ")" as string separators, with the pieces going into array "a". The first piece (a[1]) is "LINESTRING ", the second (a[2]) for the first line of "wkts" is "-44.99019 -62.15421 -44.98773 -62.14981" and the third (a[3]) is empty.
split(a[2],b," "); The string of longitudes and latitudes (a[2]) is split using one or more spaces as separator and the pieces stored in array "b". For the first line of "wkts", b[1] is "-44.99019", b[2] is "-62.15421", b[3] is "-44.98773" and b[4] is "-62.14981".
$2=sprintf("%.5f",(b[2]+b[4])/2); A second field is defined as the average of the two latitudes, printf-formatted to 5 decimal places.
$3=sprintf("%.5f",(b[1]+b[3])/2); A third field is defined as the average of the two longitudes, again printf-formatted to 5 decimal places.
$4=sprintf("%.0f",0.5*sqrt(((b[2]-b[4])*111320)^2 + ((b[1]-b[3])*111320*cos(b[2]*(pi/180)))^2)); A fourth field is defined by a complex calculation whose result is printf-formatted to be rounded with no decimal places. The calculation of the Euclidean distance between two latitude/longitude points is explained in this BASHing data post from 2018. The "111320" figure for meters per degree is based on this Wikipedia article on decimal degrees.
print " " $2 FS $3 FS $4}The three new fields are printed for each WKT with a leading space and tab separation.
There are a couple of caveats that come with this command. The first is that you should allow for the uncertainty in the WKT's two latitude/longitude points by extending the calculated uncertainty for the transect. This might be only 10 m for a good GPS reading, but I would be conservative and add 30 m to the half-length of the transect (and round up to the nearest 10 m).
The second warning is that you can't do "exact" calculations with decimal numbers on a computer, because computers calculate in binary. The calculated midpoint is an approximation and is probably good to a rounded-off 4 decimal places. How you would do that rounding is another choice; I always "round to even", but you might prefer another method. In any case, the location's uncertainty will probably be much larger than a small rounding bias or error.
Last update: 2021-12-22
The blog posts on this website are licensed under a
Creative Commons Attribution-NonCommercial 4.0 International License