
For a full list of BASHing data blog posts, see the index page. ![]()
Too many lat/lon digits
-17.6000003814697, 145.699996948242 is a latitude, longitude (lat/lon) in decimal degrees. Anyone familiar with spatial data is going to wonder why this point location has so many decimal places. No location could possibly be known that exactly. The latitude is given to the nearest 0.0000000000001 degree, or about 11 nanometres. That's roughly 1/7000 the diameter of a human hair, or roughly the length of a close-packed row of 100 silicon atoms.
This ridiculous lat/lon appears in a database at the Australian National Insect Collection. It's the location of a bug-collecting site that was described by the collectors in 1971 as "ca. 12km SE Millaa Millaa" in Queensland, Australia. The record has been published in the Atlas of Living Australia here. Here's a screenshot from that record (grabbed 2018-06-25):
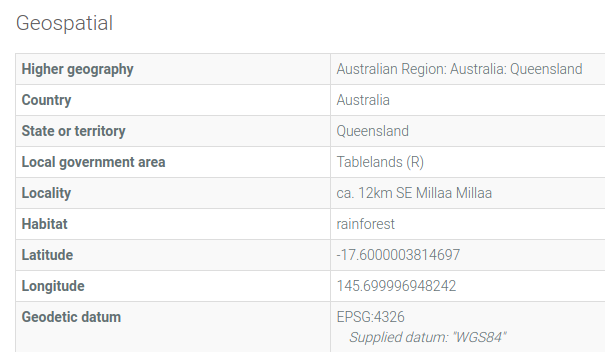
I often see too-exact lat/lon figures in my data auditing work. Only a few are as nutty as that Millaa Millaa record, but impossible 8- and 10-decimal place lat/lons are common in biodiversity databases. In my gloomier moments I doubt that the data compilers have ever heard about significant figures or understand how latitude and longitude work.
In this post I look at three causes of over-long lat/lons for point locations. I apologise in advance to spatial data specialists, because I'm going to ignore some geo-details and geo-complications.
But first... By way of introduction, please remember that latitudes and longitudes can be measures of arc length on the surface of the Earth, as well as measures of angular position. Lat/lons in this sense are something like the x,y coordinates you plotted on graphs at school. They're measured from the zero line of latitude (the Equator) and the zero line of longitude (the Prime Meridian that runs through Greenwich, England). One degree of latitude is about 111 km.
It may be easier to remember that the circumference of the Earth is about 40,000 km and that there are 360 degrees in a circle. 40000 km / 360 degrees = about 111 km per degree.
If one degree of latitude is about 111 km or about 111,000 m, then
- 0.1 degree is about 11,100 m
- 0.01 degree is about 1,110 m
- 0.001 degree is about 111 m
- 0.0001 degree is about 11 m
- 0.00001 degree is about 1.1 m
- 0.000001 degree is about 0.11 m
Wikipedia has a helpful table with more exact estimates.
The length of a degree of longitude decreases with the cosine of the latitude. At zero degrees latitude (at the Equator) it's about 111 km, and at 45 degrees (north or south) it's about 79 km.
Conversions. I suspect that most of the over-long lat/lons I see are the result of format conversions. Suppose I want to convert the latitude 41°17'59"N to decimal degrees. Yes, my calculator app can turn that into 41.299722222, but the latitude in degrees/minutes/seconds was only given to the nearest 1 second. That's 1/3600 of a degree, or about 31 m. And "41.299722222" is given to the nearest 0.000000001 degree, or about 0.1 mm. It isn't "more scientific" or "more honest" to retain all those decimal places; the last ones are meaningless. 41.2997 is an appropriate conversion. That's a latitude to the nearest 0.0001 degree, or about 11 m. If I round off to 41.300 I've gone too far, because 0.001 degree is about 111 m, and the original degrees/minutes/seconds latitude was given more exactly than that.
Google Maps and Google Earth. The Google spatial data services are very useful for getting the lat/lon of a point location, but Google's accuracy is overstated. Both Google Maps (left) and Google Earth (right) return 6-place lat/lons in decimal degrees (±5.5 cm in latitude).

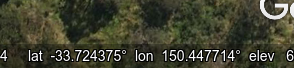
That's just not possible. The biggest source of error is Google's georegistration and rectification: the "draping" and stretching of a digital map or a satellite image on an underlying mathematical model of latitude and longitude. The trueness of the result varies from place to place and from an earlier image to a later image. You would be lucky to get a Google lat/lon less than 2-3 metres from the true lat/lon. For this reason, rounding Google lat/lons from 6 to 5 places is a necessary first step.
But that's not the whole story, because there's also an error in positioning a cursor on a Google interface, especially if the feature you're locating is not very well-defined. Rounding a Google lat/lon obtained in this way to 4 decimal places (roughly ±5 m in latitude) is just common sense.
I haven't found many published, independent investigations of Google's mapping error. A 2010 study found an average horizontal offset of almost 7 m in open country in the USA.
GPS readings. GPS units are minor contributors to the "too many digits" problem. Field biologists typically record spot locations with a consumer-grade, handheld GPS receiver, without a nearby, ground-level base station to improve accuracy. What's more, they typically take a single GPS reading. They don't take repeated readings at the location over several days and average the results. They take their single readings when and where they need to, sometimes without a clear view of the sky and sometimes with objects nearby that can bounce GPS satellite signals.
Regardless of conditions, the GPS readout says (for example) -35.72914 149.46372. That's a lat/lon to the nearest 0.00001 degree, or about 1.1 m in latitude (or ±0.55 m). Is that believable?
No, and not only because it was a single reading under conditions that might not have been ideal. In 2018, Magellan was offering 3-5 m accuracy under good conditions for its basic GPS units, while Garmin was more cautious: 5-10 metres. Garmin was also more explicit in describing what GPS accuracy really means: "Garmin GPS receivers are accurate to within 15 meters (49 feet) 95% of the time with a clear view of the sky."
Neither company would claim that single readings to 0.00001 degree on their handheld devices are spot-on. A wise user would round off the -35.72914 149.46372 on the handheld GPS unit to -35.7291 149.4637.
In a database, the original 5-place readings could be preserved if needed in a separate "raw data" field. An even better approach for field biologists is to record for each GPS reading the coordinateUncertaintyInMeters, a Darwin Core term that means "The horizontal distance (in meters) from the given decimalLatitude and decimalLongitude describing the smallest circle containing the whole of the Location". I'd add "...and also containing a conservative estimate of the error in the GPS reading".
Rounding off. This is easy enough to do manually, lat/lon by lat/lon, but if you do it on the command line you may face the ugly problem of biased vs. unbiased rounding.
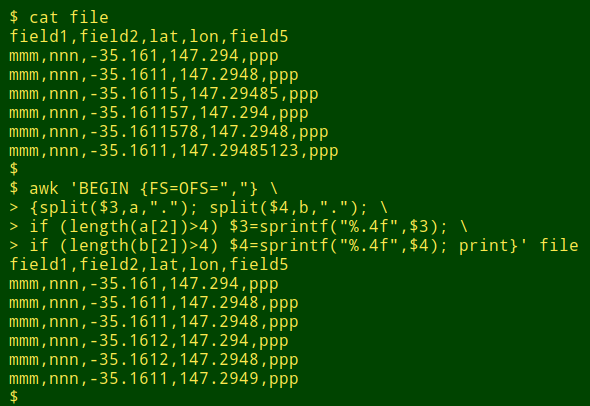
In the example below, I'm using AWK to round off lat and lon entries to 4 decimal places. First I split the entry into the parts before and after the decimal point, then test the "after" to see if it's longer than 4 characters. If it is, the entry is printed using AWK's printf to round to 4 decimal places.
awk 'BEGIN {FS=OFS=","} \
{split($3,a,"."); split($4,b,"."); \
if (length(a[2])>4) $3=sprintf("%.4f",$3); \
if (length(b[2])>4) $4=sprintf("%.4f",$4); print}' file
[file:]
field1,field2,lat,lon,field5
mmm,nnn,-35.161,147.294,ppp
mmm,nnn,-35.1611,147.2948,ppp
mmm,nnn,-35.16115,147.29485,ppp
mmm,nnn,-35.161157,147.294,ppp
mmm,nnn,-35.1611578,147.2948,ppp
mmm,nnn,-35.1611,147.29485123,ppp
As you can see above and below, AWK's printf doesn't always "round to even" when the last digit is a 5:
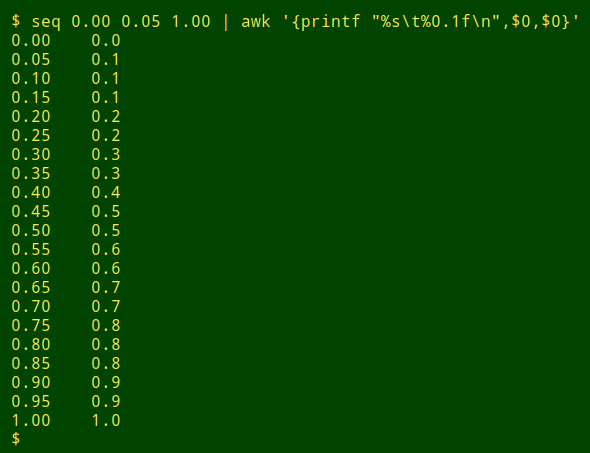
This isn't AWK's fault. As explained in the GNU AWK manual:
"The way printf and sprintf() ... perform rounding often depends upon the system’s C sprintf() subroutine. On many machines, sprintf() rounding is unbiased, which means it doesn’t always round a trailing .5 up, contrary to naive expectations. In unbiased rounding, .5 rounds to even, rather than always up, so 1.5 rounds to 2 but 4.5 rounds to 4. This means that if you are using a format that does rounding (e.g., "%.0f"), you should check what your system does."
About "trueness" You can determine the lat/lon of a place by estimation or by measurement, and as with every other kind of estimation or measurement, the lat/lon you determine may not be the true value. The closeness of your lat/lon to the true lat/lon is the "trueness" of your estimate or measurement.
If you measure the lat/lon repeatedly you're likely to get slightly different results each time. You might calculate the mean of the results and use the mean as a best guess of the true lat/lon. "Precision" is some measure of the scatter of the estimates or measurements around their mean value.
Trueness and precision are independent of each other. You can have very similar lat/lon measurements (high precision) with a mean value that's a long way off the true lat/lon (low trueness). You can also have seriously varying lat/lon measurements (low precision) which nevertheless cluster around a mean that's very close to the true value (high trueness).
The term "accuracy" was used until recently to mean trueness. It's now also used to cover trueness and precision combined.
Last update: 2018-06-30
The blog posts on this website are licensed under a
Creative Commons Attribution-NonCommercial 4.0 International License